一元三次方程求根公式推导-一元三次方程求根公式推导过程 百度百科

在探讨一元三次方程求根公式时，我们首先将方程化简为标准形式ax3+bx2+cx+d=0为了简化方程，我们引入一个变换x=yk3，其中k是待确定的系数将x替换为yk3后，得到新的方程yk33+byk32+cyk3+d=0接下来，我们逐步展开并整理方程首先，我们关注yk3。

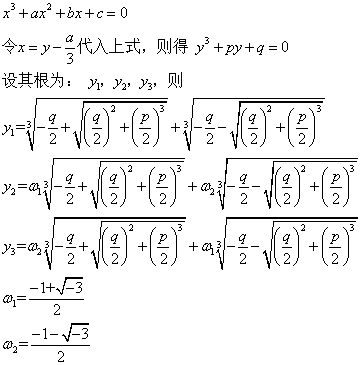
一一元三次方程求根公式 一元三次方程ax#179+bx#178+cx+d=0的求根公式较为复杂，且通常针对的是将其化简后的特殊形式对于一般形式，可以通过变量替换等方式转化为特殊形式后再应用求根公式此处不直接展示完整的求根公式，因其过于冗长且难以记忆二推导过程 特殊形式的一元三次方程。

一元三次方程求根公式如下其中 我们先讨论一类一元三次方程特殊形式通过和立方公式，可以得到求根公式推导过程将展示如下步骤令，由第三个式子两边同时乘可得到这是关于的一元二次方程根据一元二次求根公式，得解释一下是模长为，辐角为的虚数，是的一个立方根又因为所以每组解之间的。

一元三次方程解法求根公式韦达定理一元三次公式设方程为aX^3+bX^2+cX+d=0，上式除以a，并设x=yb3a，则可化为y3+py+q=0，其中p=3acb23a2，q=27a2d9abc+2b327a3可用特殊情况的公式解出y1y2y3，则原方程的三个根为x1=y1b3a，x2=y2b3a，x3=y3b。

一元三次方程的求根公式推导过程可以分为两步首先，通过配方消去二次项，将方程转换为立方和的形式接着，利用立方和公式和韦达定理，找出其他解我们以公式为例，首先将方程转化为公式，通过观察发现立方和公式中的公式仅包含一次项三次项和常数项，这对应于公式的形式然后，通过解。

由一元三次方程的完整式X#179+a1X#178+a2X+a3=0 1和缺项式X#179+pX+q=0 2可知，欲将式 1转换为式 2，需令y=Xa13代入式 1，得Xa13#179+a1Xa13#178+=0，化简后，其中含X#178的项已经抵消，这样就将问题化为了式2的形式。

一元三次方程的求根公式用通常的演绎思维是作不出来的，用类似解一元二次方程的求根公式的配方法只能将型如ax^3+bx^2+cx+d+0的标准型一元三次方程形式化为x^3+px+q=0的特殊型一元三次方程的求解公式的解法只能用归纳思维得到，即根据一元一次方程一元二次方程及特殊的高次方程的求根公式。

为求其余两个根，将y1代入原方程y^3+py+q=yy1fy中，通过待定系数法，设y^3+py+q=yy1y^2+k1y+k2，得到k1=y1，k2=p+y1^2由此求得fy=y^2+y1y+p+y1^2，进而利用求根公式解出y2和y3这个过程虽然繁琐，但正是通过这些步骤，我们能够得到一元三次方程的解。

具体来说，A和B可以通过公式A=q2+q^24+p^327^12，B=q2q^24+p^327^12来表示将这些表达式代入x=A^13+B^13，就可以得到一元三次方程x^3+px+q=0的解通过这种方法，我们不仅能够理解一元三次方程求根公式的推导过程，还能够掌握如何应用这一。

一元三次方程的求根公式为x = b plusmn radicsup3 这是经过严格的数学推导得出的通用公式，适用于解决标准形式的一元三次方程 axsup3 + bxsup2 + cx + d = 0 的求根问题对于求解特定的三次方程，只需要将方程的系数abc代入上述公式即可求解解释一元三。

一元三次方程求根公式即卡尔丹公式，用于解形如x^3+px+q=0的方程，其三个根分别为第一个根x1x1 = left left + sqrtleft^2 left right^frac13 + left left sqrtleft^2 left right^frac13$第二个根x2其中，w为复数单位的一个根，$w = frac1。

一元二次方程求根公式一元三次方程求根公式和一元四次方程求根公式的多种方法，自行发现的不同推导方法 对于一元二次方程，根可以表示为\x = \fracb \pm \sqrtb^24ac2a\系数abc之间具有对称性，即如果将方程的系数对调，得到的方程与原方程的根互为倒数这就是倒根。

一元三次方程求根公式的解法并非通过常规的演绎思维直接得出，而是通过类似解一元二次方程的求根公式的方式，将一般形式的三次方程转化为特殊形式，即x^3+px+q=0的形式为了找到这种形式的一元三次方程的解，需要采用归纳方法，从一元一次二次以及特定高次方程的求根公式的形式，归纳出一元三次方程。

这就是著名的卡丹公式 如果再由y转到x，那么，就能得到一个确定一般的三次方程的根的公式 参考资料htm。

一元三次方程求根公式通过归纳思维推导，不同于一元二次方程的直接求解方法通常的演绎思维无法直接求解一元三次方程，而需要将一般形式转化为特殊形式对于方程x^3+px+q=0，其解的形式为x=A^13+B^13将x=A^13+B^13两边立方得x^3=A+B+3AB^13A^1。

一元三次方程的一般形式是ax^3+bx^2+cx+d=0，其中abc和d是方程的系数，它们可以是实数或复数费拉里的求根公式就是对于给定的系数abc和d，可以找到三个解x1x2和x3的公式这个公式的推导过程涉及到一些高级的数学技巧，包括对特殊函数的计算和公式推导但是，对于大部分应用场景。

一元三次方程的求解方法不同于二次方程，不能通过一般的演绎思维直接得出通常需要通过归纳思维，根据已知的低次方程求根公式形式，推导出三次方程的求根公式对于标准形式的一元三次方程 \ax^3+bx^2+cx+d=0\，我们首先将其化简为 \x^3+px+q=0\ 的特殊形式在推导过程中，我们假设一。